정렬
Contents
13. 정렬¶
정렬sorting은 모음 객체에 포함된 항목들을 특정 크기 기준에 따라 오름차순 또는 내림차순으로 위치하도록 하는 과정을 말한다. 예를 들어, 문자열들로 이루어진 리스트의 항목을 알파벳 순서대로 정렬하거나 도시들의 리스트를 인구, 면적 등으로 정렬할 수 있다. 이진탐색에서 정렬된 리스트가 얼마나 유용하게 활용되는지를 확인하였다.
일반적으로 정렬 알고리즘의 시간복잡도 분석에 사용되는 기본 단위연산으로는 다음 두 가지가 사용된다.
두 값의 크기 비교 : 두 항목의 크기를 서로 비교할 수 있어야 함.
두 항목의 자리 교환 : 예를 들어, 보다 작은 값을 보다 큰 값보다 왼편에 위치하도록 해야 함.
13.1. 버블 정렬¶
버블 정렬bubble sort은 연속된 두 수를 비교하여 필요한 경우 작은 값은 왼쪽으로, 큰 값은 오른쪽으로 자리를 바꾸는 일을 리스트 끝까지 반복하는 패스pass과정을 리스트가 정렬될 때까지 반복하는 알고리즘이다. 예를 들어, 다음은 버블 정렬로 리스트를 정렬하는 첫째 패스 과정이다.
처음 두 항목을 비교한다.
5가13보다 작으므로, 자리교환은 없다.

두 번째와 세 번째 항목을 비교한다.
13이17보다 작으므로, 자리교환은 없다.

세 번째 항목과 네 번째 항목을 비교한다.
17이2보다 크므로, 자리교환을 한다.

네 번째와 다섯 번째 항목을 비교한다.
17이48보다 작으므로, 자리교환은 없다.

다섯 번째와 여섯 번째 항목을 비교한다.
48이22보다 크므로, 자리교환을 한다.

첫째 패스 과정을 거치면, 가장 큰 항목인
48이 가장 오른쪽으로 간다.

이후 둘째 패스를 실행하면, 두 번째로 큰 항목이 오른쪽에서 둘째 자리에 위치한다. 이러한 패스 과정을 길이가 n인 리스트에 대해 n-1 번 적용하면 최종적으로 오른차순으로 정렬된다.
버블 정렬
거품이 뽀글뽀글 위로 올라가bubble up는 것에 비유하여 버블 정렬이라고 부른다.
아래는 버블 정렬의 전체 패스가 작동하는 과정을 보여준다.
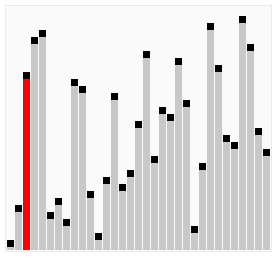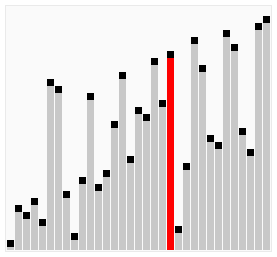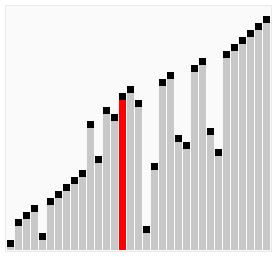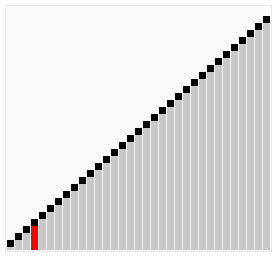
리스트를 인자로 받아 버블 정렬을 사용하여 오름차순으로 정렬된 리스트를 반환하는 bubble_sort() 함수를 정의하여라.
def bubble_sort(a_list) :
for i in range(1, len(a_list)) : #패스
for j in range(len(a_list)-i) : #패스 별 크기비교 및 자리교환
if a_list[j] > a_list[j + 1] :
a_list[j], a_list[j + 1] = a_list[j + 1], a_list[j]
a_list_bs = [5, 13, 17, 2, 48, 22]
bubble_sort(a_list_bs)
print(a_list_bs)
[2, 5, 13, 17, 22, 48]
버블 정렬에서 항목들의 비교 횟수는 1부터 n-1까지의 합이다.
패스 |
비교 횟수 |
|---|---|
\(1\) |
\(n-1\) |
\(2\) |
\(n-2\) |
\(3\) |
\(n-3\) |
\(\cdots\) |
\(\cdots\) |
\(n\)\( - \)\(1\) |
\(1\) |
총 비교 횟수는 \(1 + 2 + \cdots + (n-1) = \frac{n(n-1)}{2} = \frac{n^2}{2} - \frac{n}{2}\)로, \(O(n^2)\)의 시간복잡도를 갖는다.
버블 정렬은 코드로 구현하기 쉽지만 정렬하는 데에 다른 정렬 기법에 비해 오랜 시간이 걸리는 비효율적인 방법이다.
13.2. 선택 정렬¶
선택 정렬selection sort은 버블 정렬의 단점인 자리교환 횟수를 패스당 최대 한 번만 수행하도록 개선한 기법으로, 기본적으로 작동과정은 버블 정렬과 동일하다. 다만 자리교환을 바로 실행하는 것이 아니라 패스 별로 최솟값을 확인한 다음 최종적으로 한 번 자리교환을 실행한다. 예를 들어, 다음은 선택 정렬로 리스트를 정렬하는 과정이다.
주어진 리스트는 아래와 같다.

리스트의 최솟값은
2이다.2을 가장 왼쪽에 있는 항목과 자리교환한다.

두 번째로 작은 항목은
5이다.5는 왼쪽에서 둘째에 위치한 항목과 자리교환한다.

세 번째로 작은 항목은
13이다. 왼쪽에서 셋째 위치에 있는 항목과 자리교환한다.

다섯 번째로 작은 항목은
22이다. 왼쪽에서 다섯 번째 위치에 있는 항목과 자리교환한다.

4번의 패스를 실행하면 오름차순으로 정렬된 리스트가 생성된다.
아래는 선택 정렬의 전체 패스가 작동하는 과정을 보여준다.

리스트를 인자로 받아 선택 정렬을 사용하여 오름차순으로 정렬된 리스트를 반환하는 selection_sort() 함수를 정의하여라.
def selection_sort(a_list) :
for i in range(len(a_list)) :
min_index = i
for j in range(i + 1, len(a_list)) :
if a_list[min_index] > a_list[j] :
min_index = j
a_list[i], a_list[min_index] = a_list[min_index], a_list[i]
a_list_ss = [5, 13, 17, 2, 48, 22]
selection_sort(a_list_ss)
print(a_list_ss)
[2, 5, 13, 17, 22, 48]
선택 정렬에서의 크기 비교는 버블 정렬때와 동일하게 발생하여 시간복잡도는 \(O(n^2)\)이다. 다만, 자리교환 횟수가 최대 n-1번 발생하여 버블 정렬의 경우보다 선택 정렬이 조금 더 빠르다.
13.3. 합병 정렬¶
합병 정렬 또는 병합 정렬merge sort은 분할 정복 기법을 이용한 정렬 알고리즘으로, 합병 정렬에 사용되는 분할과 정복은 다음과 같다.
분할 : 리스트를 반복적으로 이등분해서 생성된 모든 리스트의 길이가 1이 되도록 한다.
정복 : 길이가 1인 리스트는 이미 정렬되어 있으므로, 그런 리스트 두 개를 합쳐서 새로운 정렬 리스트를 만들며, 이 과정을 반복해서 최종적으로 원래 리스트에 포함된 항목을 정렬시킨 새로운 리스트를 얻게 된다.
아래는 합병 정렬이 작동하는 과정을 보여준다.

분할 과정
리스트를 인자로 받아 리스트의 길이가 1일 될 때까지 이등분을 반복하는 merge_sort() 함수를 정의하여라. 이는 아래와 같이 재귀를 사용하여 구현할 수 있다.
def merge_sort(a_list) :
if len(a_list) > 1 :
mid = len(a_list) // 2
left_half = a_list[:mid]
right_half = a_list[mid:]
merge_sort(left_half)
merge_sort(right_half)
합병 과정
합병 과정은 분할 과정보다 어렵다. 이미 정렬된 두 개의 리스트를 합쳐서 정렬된 새 리스트를 만들어야 한다. 이를 위해 두 리스트의 항목을 하나씩 비교해서 작은 수를 먼저 새로운 리스트에 추가하는 알고리즘을 사용한다.
i, j, k = 0, 0, 0
while i < len(left_half) and j < len(right_half):
if left_half[i] <= right_half[j]:
a_list[k] = left_half[i]
i = i + 1
else:
a_list[k] = right_half[j]
j = j + 1
k = k + 1
위 합병 과정이 끝난 후 한 쪽 리스트에 항목이 남아 있다면 그대로 그 항목들이 더 큰 값들이기에 이어서 추가해주면 된다.
while i < len(left_half):
a_list[k] = left_half[i]
i = i + 1
k = k + 1
while j < len(right_half):
a_list[k] = right_half[j]
j = j + 1
k = k + 1
하나의 코드로 정리하면 다음과 같다.
def merge_sort(a_list):
# 분할 과정
print("분할", a_list)
if len(a_list) > 1:
mid = len(a_list) // 2
left_half = a_list[:mid]
right_half = a_list[mid:]
merge_sort(left_half)
merge_sort(right_half)
# 합병 과정
i, j, k = 0, 0, 0
while i < len(left_half) and j < len(right_half):
if left_half[i] <= right_half[j]:
a_list[k] = left_half[i]
i = i + 1
else:
a_list[k] = right_half[j]
j = j + 1
k = k + 1
while i < len(left_half):
a_list[k] = left_half[i]
i = i + 1
k = k + 1
while j < len(right_half):
a_list[k] = right_half[j]
j = j + 1
k = k + 1
print("합병", a_list)
a_list_ms = [6, 5, 3, 1, 8, 7, 2, 4]
merge_sort(a_list_ms)
print(a_list_ms)
분할 [6, 5, 3, 1, 8, 7, 2, 4]
분할 [6, 5, 3, 1]
분할 [6, 5]
분할 [6]
합병 [6]
분할 [5]
합병 [5]
합병 [5, 6]
분할 [3, 1]
분할 [3]
합병 [3]
분할 [1]
합병 [1]
합병 [1, 3]
합병 [1, 3, 5, 6]
분할 [8, 7, 2, 4]
분할 [8, 7]
분할 [8]
합병 [8]
분할 [7]
합병 [7]
합병 [7, 8]
분할 [2, 4]
분할 [2]
합병 [2]
분할 [4]
합병 [4]
합병 [2, 4]
합병 [2, 4, 7, 8]
합병 [1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
합병 정렬의 분할 과정에서는 \(\log_2 n\)번 분할이 발생하며, 크기 비교나 자리 교환은 하지 않는다. 반면, 두 개의 리스트를 합쳐서 길이가 \(m\)인 리스트를 생성할 때 필요한 연산은 항목 비교와 항목 업데이트이며, 이는 \(O(m)\)의 시간복잡도를 갖는다. 따라서, 합병 정렬의 시간복잡도는 \(O(n\log n)\)이다.
13.4. 퀵 정렬¶
퀵 정렬quick sort은 합병 정렬과 마찬가지로 분할 정복 기법을 사용하는 알고리즘으로, 분할 과정이 경우에 따라 이등분이 아닌 한쪽으로 치우치는 방식으로 진행될 수 있다.
퀵 정렬은 분할과 정복을 동시에 진행하는 데, 피벗pivot, 기준값으로 지정된 값보다 작은 값들은 피벗 왼쪽으로, 같거나 큰 값들은 피벗 오른쪽으로 이동시킨다. 피벗으로 사용된 값의 위치를 기준으로 좌우 두 개의 부분 리스트로 분할한 후 동일 과정을 재귀적으로 반복한다.
피벗 지정
피벗은 리스트의 임의의 값을 사용해도 되지만 여기서는 오른쪽 맨 끝에 위치한 값을 사용한다. 경우에 따라 양끝과 중앙에 위치한 세 값의 중앙값을 사용하거나 왼쪽 맨 끝, 또는 중앙에 위치한 값 등을 사용하기도 한다.
분할 정복
분할과 정복을 동시에 진행하며, 한 번의 분할 과정을 통해 두 개의 보다 작은 리스트로 분할한 후에 분할된 두 개의 리스트에 대해 분할과 정복을 재귀적으로 진행한다.
예를 들어, 다음은 퀵 정렬로 리스트를 정렬하는 과정이다.
주어진 리스트는 아래와 같다.

리스트의 오른쪽 맨 끝에 위치한 값을 피벗으로 사용하기로 했으므로, 피벗은
22이다.

왼쪽부터
22보다 큰 항목을 찾으면48이고, 오른쪽부터22보다 작은 항목을 찾으면5이다. 두 항목을 자리교환한다.

다시 왼쪽부터
22보다 큰 항목을 찾으면23이고, 오른쪽부터22보다 작은 항목을 찾으면2이다. 두 항목을 자리교환한다.

다시 왼쪽부터
22보다 큰 항목을 찾으면23이고, 오른쪽부터22보다 작은 항목을 찾으면17이다. 그런데, 오른쪽부터 찾은17의 위치가 왼쪽부터 찾은23의 위치보다 왼쪽에 있다. 즉, 서로 엇갈린다. 이련 경우, 둘 중 큰 항목인23과 피벗22를 자리교환한다.

한 번의 분할과정을 통해 두 개의 작은 리스트로 분할되었다. 이제 두 개의 작은 리스트에 대해 위의 과정을 반복한다.
아래는 퀵 정렬이 작동하는 과정을 보여준다.

리스트를 인자로 받아 퀵 정렬을 사용하여 오름차순으로 정렬된 리스트를 반환하는 quick_sort() 함수를 정의하여라.
def quick_sort(a_list, first, last) :
if first >= last :
return
pivot = last
left = first
right = last - 1
while left <= right :
print(a_list)
while a_list[left] < a_list[pivot] :
left += 1
while a_list[right] > a_list[pivot] :
right -= 1
if left > right :
a_list[left], a_list[pivot] = a_list[pivot], a_list[left]
else :
a_list[left], a_list[right] = a_list[right], a_list[left]
quick_sort(a_list, first, left - 1)
quick_sort(a_list, left + 1, last)
a_list_qs = [48, 23, 17, 2, 5, 22]
quick_sort(a_list_qs, 0, len(a_list_qs) - 1)
print(a_list_qs)
[48, 23, 17, 2, 5, 22]
[5, 23, 17, 2, 48, 22]
[5, 2, 17, 23, 48, 22]
[5, 2, 17, 22, 48, 23]
[5, 2, 17, 22, 48, 23]
[2, 5, 17, 22, 48, 23]
[2, 5, 17, 22, 23, 48]
피벗을 기준으로 분할할 때 이상적인 경우 기존의 리스트를 거의 이등분한다. 이 경우 분할 횟수는 \(\log n\)이다. 여기서 \(n\)은 입력 리스트의 길이를 나타낸다. 그리고 한 번 분할할 때마다 피벗과 나머지 값들이 비교되고 필요에 따라 자리교환이 발생하는 데 이에 대한 시간복잡도는 \(O(n)\)이다. 따라서 최선의 경우 퀵 정렬 알고리즘의 시간복잡도는 \(O(n\log n)\)이다. 하지만 최악의 경우, 분할이 한쪽으로 쏠릴 수도 있다. 예를 들어, 거의 정렬되어 있는 리스트일 경우 피벗을 기준으로 1대 n-1개의 부분 리스트로 분할될 수 있다. 이런 경우, \(n\)번에 가까운 분할이 필요하며, 시간복잡도는 \(O(n^2)\)이 나온다.
13.5. 연습 문제¶
13.5.1. 문제¶
A는 문서 정렬을 하기로 했다. 문서 이름 형식은 다음과 같다. 가장 먼저 문서의 버전이 숫자로 적혀있고, 그 다음은 문서의 제목이 공백없이 적혀있다. 그리고 중요 문서라 제목에 오탈자가 나는 것을 방지하기 위해 동일한 제목이 공백없이 역순으로 적혀있다. 즉, 문서 이름의 구성은 (버전)(문서제목)(역순문서제목)이다. 문서의 버전이 높을 수록 최신 문서이다.
제목이
testresult이고 버전이 1인 문서
1testresulttlusertset
제목이
testresult이고 버전이 3인 문서
3testresulttlusertset
제목이
personalinformation이고 버전이 2인 문서
2personalinformationnoitamrofnilanosrep
문서 이름 리스트를 입력 받아, 문서 제목의 알파벳 순서대로 정렬된 리스트를 반환하는 docu_sort()함수를 버블정렬을 사용하여 정의하여라. 단, 문서 제목은 모두 알파벳 소문자로 되어 있고, 문서 정렬은 역순문서제목은 무시하고 문서 제목만을 기준으로 삼으며, 문서 제목이 같은 경우, 입력받은 순서를 유지한다. 또, 버전은 1부터 99사이의 숫자이고, 문서 제목이 a와 ab인 경우, a를 먼저 정렬한다.
>>> print(docu_sort(['1testtset', '3resulttlusre', '12testtset', '1finishedprojecttcejorpdehsinif', '3finishhsinif', '5personalinformationnoitamrofnilanosrep', '7abccba']))
['7abccba', '3finishhsinif', '1finishedprojecttcejorpdehsinif', '5personalinformationnoitamrofnilanosrep', '3resulttlusre', '1testtset', '12testtset']
13.5.2. 문제¶
어린이 합창단 A와 B는 마지막 곡을 함께 부르기로 했다. 두 합창단은 키 순서대로 무대에 입장하는 데, 마지막 곡을 부르기 위해 키를 기준으로 두 줄로 선 합창단 A와 B는 한 줄로 서야 한다. 합창반 선생님은 다음과 같은 방식으로 두 줄을 한 줄로 합치려고 한다. 단, 합창단 A와 B는 중복된 키가 없고, 각각은 정렬되어 있다고 가정한다.
“우선 새로운 빈 줄을 만든다. A팀의 가장 작은 아이와 B팀의 가장 작은 아이의 키를 비교한 다음, 더 작은 아이가 새로운 줄로 간다. 그 이후에 다시 남은 아이들 중 A팀에서 가장 작은 아이와 B팀에서 가장 작은 아이를 비교한 뒤 더 작은 아이가 새로운 줄의 뒤쪽에 선다. 이런 식으로 원래의 한 줄이 모두 없어질 때까지 한 뒤, 남아있는 다른 줄의 아이는 모두 그대로 한 명씩 새로운 줄의 뒤쪽으로 간다.”
A와 B 합창단원의 이름과 키가 딕셔너리 형태로 주어졌을 때, 두 딕셔너리를 입력 받아 키 순으로 정렬된 이름 리스트를 반환하는 merge_chorus()함수를 정의하여라. 이때, 줄이 합쳐지는 과정도 보여줘라.
>>> A = {"민우": 1, "지우": 2, "자연": 3, "윤지":10, "가현": 20, "마영": 30}
>>> B = {"다훈": 5, "재영": 7, "동석": 12, "수호":22, "윤우": 32}
>>> merge_chorus(A, B)
민우
민우, 지우
민우, 지우, 자연
민우, 지우, 자연, 다훈
민우, 지우, 자연, 다훈, 재영
민우, 지우, 자연, 다훈, 재영, 윤지
민우, 지우, 자연, 다훈, 재영, 윤지, 동석
민우, 지우, 자연, 다훈, 재영, 윤지, 동석, 가현
민우, 지우, 자연, 다훈, 재영, 윤지, 동석, 가현, 수호
민우, 지우, 자연, 다훈, 재영, 윤지, 동석, 가현, 수호, 마영
민우, 지우, 자연, 다훈, 재영, 윤지, 동석, 가현, 수호, 마영, 윤우
['민우', '지우', '자연', '다훈', '재영', '윤지', '동석', '가현', '수호', '마영', '윤우']
파이썬 3.7이후부터 dict는 삽입 순서를 기억한다. 즉, 딕셔너리의 값value 순서대로 딕셔너리에 항목을 추가한 다음, 값들을 확인하면 그 순서대로 있는 것을 확인할 수 있다.
A = {"민우": 1, "지우": 2, "자연": 3, "윤지":10, "가현": 20, "마영": 30}
print(list(A.items()))
[('민우', 1), ('지우', 2), ('자연', 3), ('윤지', 10), ('가현', 20), ('마영', 30)]
13.5.3. 문제¶
A 회사는 선착순으로 사은품을 제공하기 위해 도착 순서대로 번호표를 나누어 줬고, 일정 시간이 지난 후 사은품을 제공하기로 했다. 시간이 되어 담당자가 와서 보니, 고객들이 임의의 순서대로 줄을 서 있었고, 일부 고객들은 없었다. 담당자는 번호가 작은 순서대로 현장에 있는 고객들을 줄 짓고 앞에 있는 n명에게 사은품을 제공해야 한다. 담당자는 혼잡을 줄이고, 고객들을 줄 세우기 위해 다음과 같은 방법을 생각해 냈다.
“두 번째 사람이 자기보다 작은 번호를 가진 사람이 등장할 때까지 앞 사람과 자리를 바꾼다. 첫 번째 자리로 오면 비교를 중지한다. 세 번째 사람부터 앞 사람들과 비교하여 자기 자리를 찾아 들어가는 과정을 반복한다.”
임의로 서 있는 번호 리스트와 사은품의 개수를 입력 받아, 위의 방법대로 정렬된 리스트와 마지막으로 사은품을 수령하는 번호를 튜플로 묶어 반환하는 event_sort() 함수를 정의하여라.
>>> print(event_sort([1, 5, 3, 8, 2, 7, 6], 6))
([1, 2, 3, 5, 6, 7, 8], 7)
삽입 정렬insertion sort
위 문제에서 소개한 정렬 방법을 삽입 정렬이라고 부른다. 이 알고리즘을 k번 반복하면, 앞부터 k개는 정렬된다. 즉, 세 번째 사람을 정렬하기 전에 앞의 두 사람은 오름차순으로 정렬된 상태이며, 세 번째 사람이 자기 자리를 찾아가면, 세 사람은 오름차순으로 정렬된다.
이미 정렬되어 있는 데이터에 새로운 데이터를 순서에 맞게 넣을 때, 삽입 정렬을 사용하고, 거의 정렬되어 있을 때 삽입 정렬을 사용하면 매우 빠르게 동작한다.
13.5.4. 문제¶
어구전철anagram, 애너그램은 문자의 순서를 변경하여 다른 단어나 문장을 만드는 놀이로, 때로는 암호로 사용하기도 한다. 예를 들어, ‘자문’ - ‘문자’, ‘listen’ - ‘silent’, ‘TOM MARVOLO RIDDLE’ - ‘I AM LORD VOLDEMORT’ 등이 있다.
(1) 파이썬의 sort(sorted(), .sort() 등)를 사용하지 않고, 두 개의 문자열을 입력 받아 어구전철인지를 판별하는 is_anagram() 함수를 정의하여라. 어구전철을 확인할 때, 공백은 무시한다.
>>> print(is_anagram('문자', '주문'))
False
>>> print(is_anagram('문자', '자문'))
True
>>> print(is_anagram('listen', 'silent'))
True
>>> print(is_anagram('eat', 'ate'))
True
(2) 파이썬의 sorted()함수를 사용하여, 위의 함수를 정의하여라.
13.5.5. 문제¶
정수 리스트를 인자로 받아서 리스트의 각 항목을 조합하여 만들 수 있는 가장 작은 수를 반환하는 함수 min_num()을 정의하라.
(단, 정수 리스트의 항목은 모두 사용해야 하며, 정렬해주는 함수나 메서드를 사용하지 않는다.)
예를 들어, 2, 7, 10을 조합하여 만들 수 있는 가장 작은 수는 1027이고, 32, 121, 9, 10, 4를 조합하여 만들 수 있는 가장 작은 수는 101213249이다.
[참고] 파이썬은 문자열을 비교할 때 맨 앞 문자부터 비교한다. 숫자라면 123이 21보다 크지만 문자열은 ‘123’이 ‘21’보다 작다.
>>> print(123 < 21)
False
>>> print('123' < '21')
True
입력값으로 정수들이 공백을 기준으로 들어온다.
입력값1
2 7 10
출력값1
1027
입력값2
32 121 9 10 4
출력값2
101213249